casos de factoreo

Caso II

- Factor común por agrupación de términos

Para trabajar un polinomio por agrupación de términos, se debe tener en cuenta que son dos características las que se repiten. Se identifica porque es un número par de términos. Para resolverlo, se agrupan cada una de las características, y se le aplica el primer caso, es decir:
ejemplo:

1) 2y + 2j +3xy + 3xj =
(2y+2j)+(3xy+3xj)=
2(y+j)+3x(y+j)=
(2+3x)(y+j)

2) 5x4y + 3x2y -9xy -15xy2
5x4y -15xy2 + 3x3y -9y=
5xy (x3 -3y) +3y (x3 -3y)=
(x3 -3y)(5xy +3y)

3) 20ac + 15bc +4ad + 3bd =
(20ac + 4ad) + (15bc + 3bd) =
4a(5c + d) + 3b(5c + d)=
(4a + 3b)(5c + d)

4) 18a3 + 12a2 - 15a - 10 = (
18a3 + 12a2) - (15a + 10) =
6a2(3a + 2) - 5(3a + 2)=
(6a2 - 5)(3a + 2)

5 .a2 + ab= a(a+b)
b+b2= b(1+b)
x2+x: x(x+1)
3a2-a2= a2(3a-1)
x3-4x4: x3(1-4x)

ejercicios por resolver:

a² + ab + ax + bx

2ab + 2a - b - 1

3x² - 3bx + xy - by

3a - b² + 2b²x - 6ax

ac - a - bc + b + c² - c

6ac - 4ad - 9bc + 6bd + 15c² - 10cd

a³ + a² + a + 1

Caso III

- Trinomio cuadrado perfecto

Se identifica por tener tres términos, de los cuales dos tienen raíces exactas, y el restante equivale al doble producto de las raíces. Para solucionar un T.C.P. debemos organizar los términos dejando de primero y de tercero los términos que tengan raíz cuadrada, luego extraemos la raíz cuadrada del primer y tercer término y los escribimos en un paréntesis, separandolos por el signos que acompaña al segundo término, al cerrar el paréntesis elevamos todo el binomio al cuadrado.
Ejemplo:

x² + 6x + 9 = (x + 3)²

x                3
      2.3.x
         6x

x² + 2x + 1 = (x + 1)²

x            1
    2.1.x
      2x

x²   - 10x   +   25 = (x - 5)²

x                   (-5)
      2.(-5).x
        -10x

9x² + 30x + 25 = (3x + 5)²

3x                  5
       2.5.3x
          30x
x⁶ + 10x³ + 25 = (x³ + 5)²

x³                  5
       2.x³.5
        10x³

^{ejercios para resolver}

Extrayendo la raíz cuadrada del primer y último término y agrupándolos en un paréntesis separados por el signo del segundo término y elevando al cuadrado nos queda:

( 2x - 5y )^2

Caso IV

Diferencia de cuadrados perfectos

Se identifica por tener dos términos elevados al cuadrado y unidos por el signo menos. Se resuelve por medio de dos paréntesis, (parecido a los productos de la forma), uno positivo y otro negativo. En los paréntesis deben colocarse las raíces. Ejemplo:

EJEMPLO 1: (Todos los términos son positivos)

x3 + 6x2 + 12x + 8 = (x + 2)3

x 2

3.x2.2 3.x.22

6x2 12x

EJEMPLO 2: (Con términos negativos)

x3 - 9x2 + 27x - 27 = (x - 3)3

x -3

3.x2.(-3) 3.x.(-3)2

-9x2 27x

EJEMPLO 3: (Con todos los términos negativos)

-x3 - 75x - 15x2 - 125 = (-x - 5)3

-x -5

3.(-x)2.(-5) 3.(-x).(-5)2

-15x2 -75x

EJEMPLO 4: (Con fracciones)

x3 + 3/2 x2 + 3/4 x + 1/8 = (x + 1/2)3

x 1/2

3.x2. 1/2 3.x.(1/2)2

3/2 x2 3/4 x

EJEMPLO 5: (Con un número multiplicando a la x3)

64x3 + 144x2 + 108x + 27 = (4x + 3)3

4x 3

3.(4x)2.3 3.4x.32

144x2 108x

EJERCICIOS PARA RESOLVER

a3b3 + 3a2b2x + 3abx2 + x3 =

x6 + 6x4 + 12x2 + 8 =

3/4 x4y2 - 1/8 x6y3 + 1 - 3/2 x2y =

5x3 + 6x2 + 12 x + 8 =

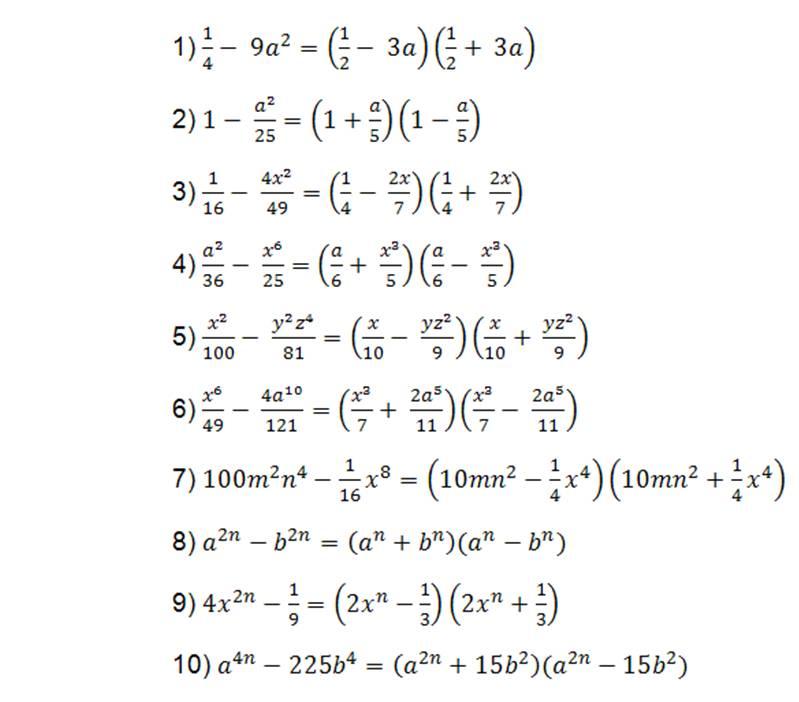
Caso V

Trinomio cuadrado perfecto por adición y sustracción

Se identifica por tener tres términos, dos de ellos son cuadrados perfectos, pero el restante hay que completarlo mediante la suma para que sea el doble producto de sus raíces, el valor que se suma es el mismo que se resta para que el ejercicio original no cambie. Para solucionarlo, se usan como ayuda los casos número III y IV. para moldar debe de saber el coseno de la raíz de la suma de dos polimo x que multiplicado sale igual a la raíz de 2.

Se identifica por tener tres términos, hay una literal con exponente al cuadrado y uno de ellos es el término independiente. Se resuelve por medio de dos paréntesis, en los cuales se colocan la raíz cuadrada de la variable, buscando dos números que multiplicados den como resultado el término independiente y sumados (pudiendo ser números negativos) den como resultado el término del medio.

Ejemplo :

x2 - 9 = (x + 3).(x - 3)

x 3

x2 - y2 = (x + y).(x - y)

x y

b2 - 1 = (b + 1).(b - 1)

b 1

x2 - 9/25 = (x + 3/5).(x - 3/5)

x 3/5

ejercicios por resolver

36x2 - a6b4 =

x2 - 0,16 =

-x2 + 4 = 4 - x2 =

4/25 x6a2 - 0,01 b4y10 =

x2 - 3 =

Caso VI - Trinomio de la forma x² + bx + c

Se identifica por tener tres términos, hay una literal con exponente al cuadrado y uno de ellos es el término independiente. Se resuelve por medio de dos paréntesis, en los cuales se colocan la raíz cuadrada de la variable, buscando dos números que multiplicados den como resultado el término independiente y sumados (pudiendo ser números negativos) den como resultado el término del medio.

Ejemplo:

EJEMPLO 2: (Resta de Potencias Impares)

x3 - 8 = (x - 2).(x2 + 2x + 4)

x 2

b4 - 81 = (b - 3).(b3 + 3b2 + 9b + 27) ó (b + 3).(b3 - 3b2 + 9b - 27)

b 3

4: (Suma de Potencias Pares)

x4 + 16 = x4 + 16

5: (Con el "1")

x7 + 1 = (x + 1).(x6 - x5 + x4 - x3 + x2 - x + 1)

x 1

ejercicios por resolver:

x7 - y7 =

x6 - 1/64 =

x5 + 0,00001

-125 + x3 =

-x6 + 64 =

8x3 + 27 =

x6 + 64 =

x7 + 128a7 =

Caso VII - Trinomio de la forma ax² + bx + c

En este caso se tienen 3 términos: El primer término tiene un coeficiente distinto de uno, la letra del segundo término tiene la mitad del exponente del término anterior y el tercer término es un término independiente, o sea sin una parte literal, así:

ejemplo:

4x2 + 8x + 3
= 4x2 + 6x + 2x + 3
= (4x2 + 6x) + (2x + 3)
= 2x(2x + 3) + (2x + 3)
= (2x + 1)(2x + 3)

2x2 + 5x + 3
= 2x2 + 3x + 2x + 3
= x(2x+3) + (2x + 3)
= (2x + 3) ( x + 1)

6x2 + 7x + 2
= 6x2 + 4x + 3x + 2
=2x(3x + 2)+(3x + 2)
=(2x + 1)(3x + 2)

6x2 + 5x - 4
= 6x2 + 8x - 3x - 4
= (6x2 + 8x) - (3x + 4)
= 2x(3x + 4) - (3x + 4)
= (2x - 1)(3x + 4)

6x2+17x+12
= 6x2 + 8x + 9x + 12
= (6x2 + 8x) + (9x + 12)
= 2x(3x + 4) + 3(3x + 4)
= (2x + 3)(3x + 4)

ejercicios por resolver:

)

Caso 8 - Cubo perfecto de binomios

Podemos asegurar que una expresión algebraica es un cubo perfecto si cumple las siguientes condiciones:

Posee cuatro términos

° El primer y cuarto término son cubos perfectos (tienen raíces cúbicas exactas).

° El segundo termino sea el triple del cuadrado de la raíz cúbica del primer término multiplicado por la raíz cúbica del último término.

° El tercer termino sea el triple del cuadrado de la raíz cúbica del último término -multiplicado por la raíz cúbica del primer término.

° Los signos son todos mas o también podría ser positivo el primero y el tercero y negativo el segundo y el cuarto.

Para factorizar un cubo perfecto se forma un binomio y se eleva al cubo, el primer término del binomio es la raíz cúbica del primer término y el segundo término es la raíz cúbica del último término. El signo del segundo término es mas si todos los signos del cubo son mas y es menos si los signos del segundo y cuarto término del cubo son menos.

ejemplo:

a³ + 3 a²b + 3 a b² + b³ = (a + b)³

a³ + 3 a² + 3 a + 1 = ( a + 1)³

8 - 36 X + 54 X² - 27 X³ = ( 2 – 3X)³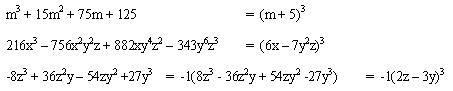

^{ejercicios por resolver:}

a³ + 1

x³ + 1

y³ + 1

a³b³x³ + 1

a³ + 8

m³ + 27

x³ + 125

n³ + 1.000

m³ + 8a³x³

x³ + y³

Caso 9 Diferencia de potencias de igual grado con exponente impar

En éste caso; la diferencia de potencias de igual grado de exponente impar únicamente es divisible por la diferencia de sus bases.

Ejemplo:

P(x) = x⁵ + 2⁵

como el exponente es IMPAR y el signo POSITIVO, el divisor será (x + 2).

x⁵ + 0 x⁴ + 0 x³ + 0 x² + 0 x + 32

completamos el polinomio para aplicar Ruffini.

EJERCICIOS PARA RESOLVER

a4 - 1

n4 - 81

b4 - 625

a4 - b4c4

x4 - y4

m4 - n4

a4x4 - m4

x4 - 16m4n4

16m4 - 81n4

81x4 - 16y4

POTENCIAS IGUALES

:
El número de monomios que la conforma son dos (2).
La raiz del primer y segundo monomio tienen que ser raíces n- ésimas diferentes a raíces cuadradas o cúbicas.
Válido para operaciones tanto de suma como de resta entre los monomios.

PASOS PARA EL DESARROLLO DE LA FACTORIZACIÓN:

Organizar los monomios de mayor a menor exponente.
Sacar la raíz n-ésima al primer y segundo término.
Dividir la expresión original entre la suma o resta (de acuerdo al signo del segundo término) de las raíces.
Igualar éste término a la suma de los (n-1) monomios en donde se observa que el primer termino comienza elevado a la (n-1) y termina en 0, mientras que el segundo término comienza en 0 y termina en (n-1).
Pasar a multiplicar el término ubicado en el denominador a la expresión obtenida en el paso anterior.
Verificar que la expresión da el ejercicio que se quiere desarrollar.

EJEMPLO:
FACTORIZAR: (m5 + n5) / (m +n )

SOLUCIÓN:

(m5 + n5) / (m + n ) = m4 – m3 n + m2 n2 - m n3 + n4
(m5 + n5) = (m + n ) . (m4 – m3 n + m2 n2 - m n3 + n4)

ejercicios para resolver:

FACTORIZACIÓN POR ASPA SIMPLE

Método de Aspa Simple
Es un método que permite factorizar trinomios de la forma: ax² + bxy + c
18x² -15x -187
➊ Descompón en sus factores los números de los extremos del trinomio

18x² - 15x -187
6x.......... 17
3x............-11

➋ Esos números que has puesto multiplicalos en forma cruzada (6x)(- 11) y (3x)(17); y pon los resultado al costado y súmalos, así:

18x² - 15x -187
6x...............17 → 51x
3x..............-11 → - 66x
------------------------------
......................- 15x

➌ Fíjate que la "suma" debe ser igual al 2do termino del trinomio (-15x). Si no lo es, entonces debes cambiar los números que has puestos, o sino cambia sus signos o hacer ambas cosas a la vez. En este caso nos dio el número buscado

➍ Agrupa dentro de un paréntesis los números unidos por los [……….], es decir agrupa como factores los números que están en forma horizontal

(6x + 17) (3x - 11)

Este es el resultado ==========================
18x² - 17x -187 = (6x + 17) (3x - 11)
==========================

Desarrolla los ejercicios:

§ x² - 5x - 6

4x² – 12xy + 5y²

x² + 7x + 12

§ 6x² - 7xy – 20y²

§ x² + 5x + 6

12x² - 8xy – 15y²

x² – 2x - 15

X² + 8xy + 7y²

x² + 2xy – 35y²

FACTORIZACIÓN POR ASPA SIMPLE

Desarrolla los ejercicios:

§ x² - 5x - 6

4x² – 12xy + 5y²

x² + 7x + 12

§ 6x² - 7xy – 20y²

§ x² + 5x + 6

12x² - 8xy – 15y²

x² – 2x - 15

X² + 8xy + 7y²

x² + 2xy – 35y²

casos de factoreo

martes, 17 de junio de 2014

POTENCIAS IGUALES

FACTORIZACIÓN POR ASPA SIMPLE

FACTORIZACIÓN POR ASPA SIMPLE

No hay comentarios:

Publicar un comentario

Archivo del blog